Function

f(x,y) = px+q

Domain

x and y are elements of the set of all Real numbers

Graphs

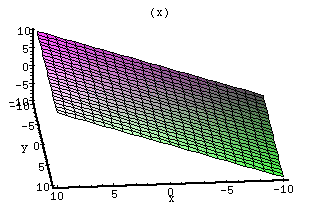
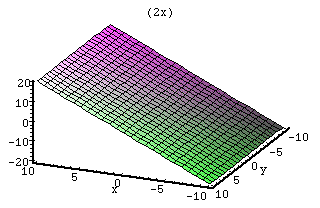
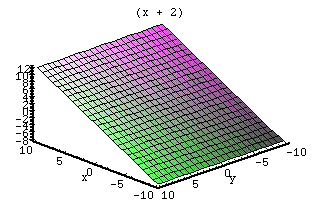
Derivative

With respect to x: p
With respect to y: 0

Critical points are formed where the two derivatives equal 0. These critical points may be minimums, maximums, or saddle points. In the first graph, for x, p = 1 and will never equal 0. Therefore, there will be no critical points for this graph. This is shown since there is no saddle point and the curve goes from negative to positive infinity.

Integral

With respect to x: ( ¹/₂ )px² + qx
With respect to y: (px + q)y

Interesting Features

This function is a plane that has a constant value for z for all y values for x. This plane goes up at a constant value. This "slope" is scaled by p. The q value changes the intercept value. As q increases, the position of the plane is lifted.