Function

f(x,y) = px² + qxy + ry²

Domain

x and y are elements of the set of all Real numbers

Graphs

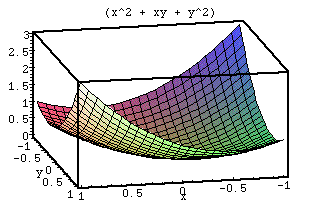
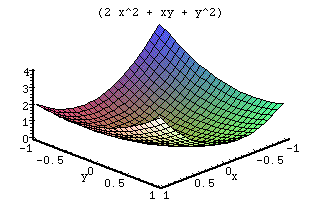
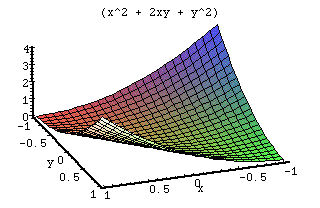
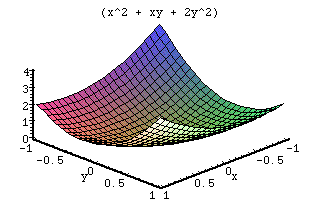
Derivative

With respect to x: 2px + qy
With respect to y: qx + 2ry

Critical points are formed where the two derivatives equal 0. These critical points may be minimums, maximums, or saddle points. In the first graph, for x² + xy + y², 0 = 2x + y which happens only when x and y are both 0. For y, 0 = x + 2y only when x and y are both 0. Therefore the only critical point is (0,0) which is the lowest point, 0.

Integral

With respect to x: ( ¹/₃ )px³ + ( ¹/₂ )px²y + ry²x + c
With respect to y: px²y + ( ¹/₂ )qxy² + ( ¹/₃ )rq³ + c
Double Integral: ( ¹/₃ )px³y + ( ¹/₄ )qx²y² + ( ¹/₃ )ry³x
Break down, first with respect to x: ( ¹/₃ )px³ + (¹/₂ )qx²y + ry²x

This is taken then with respect to y and the final double integral is returned. The double integral allows us to find the volume of an area under a surface and the xy plane. Looking at two examples, we want to find the area bound by x from -1 to 1 and y from -1 to 1 in the first graph. We first evaluate the first breakdown from -1 to 1. The second integral is then taken and evaluated from -1 to 1. For our first graph, the volume from x=-1..1 and y=-1..1 is ( ⁸/₃ ). If we look at the volume from x=0..1 and y=0..1, the process is repeated, and the volume is ( ¹¹/₁₂ ).

Interesting Features

When working with this function, there are many different items to look at. The general formula forms a curved surface that gets the lowest at the origin (0,0). Since the values are squared, the negatives become positive and the curve appears symmetric. The p scales one end of the curve causing it to rise. The q value scales the values in a symmetric manner effecting x and y. The r functions exactly the same as p only on the other axis.