Function

f(x,y) = p cos(qy)

Domain

x and y are elements of the set of all Real numbers

Graphs

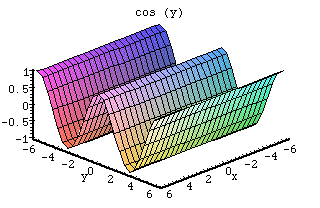
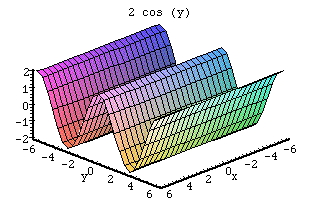
Derivative

With respect to x: 0
With respect to y: -p sin(qy)q

Critical points are formed where the two derivatives equal 0. These critical points may be minimums, maximums, or saddle points. In the first graph, for y, 0 = sin(y) which happens at n*Pi, for all n. For x, 0 = 0 for all x values. From the graph, it shows that the lines for y = n*Pi are the ridges that run high and low.

Integral

With respect to x: p cos(qy)x
With respect to y: (sin(qy)p)/q

Interesting Features

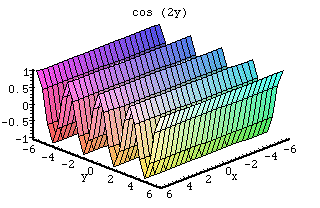
When working with this function, there are many different items to look at. The p scales the values up and down. If it is left out, the graph goes from -1 to 1. The graph goes from -p to p. This is shown in the graph of 2 cos(y). The q value scales the angle. If it is left out, the values remain the same as the angle. This means that the graph completes one cycle in 2*Pi radians. The graph of cos (2y) shows this when the angles are doubled, the graph completes one cycle in only Pi radians.