Function

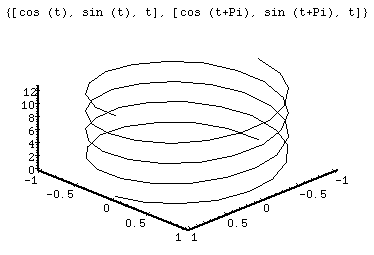
{[ x(t) = cos(t), y(t) = sin(t), z(t) = t ], [ x(t) = cos(t+Pi), y(t) = sin(t+Pi), z(t) = t ]}

Domain

t is an element of the set of all Real numbers

Graphs

Derivative

With respect to t: {[-sin(t), cos(t), 1], [sin(t), -cos(t), 1]}

Critical points are formed where all the derivatives equal 0. These critical points may be minimums, maximums, or saddle points. Since 1 will never equal 0, there will be no critical points. This means that there are no minimum or maximum points. This is the same for both equations.

Integral

With respect to t: {[sin(t), -cos(t), ( ¹/₂ )t²], [-sin(t), cos(t), ( ¹/₂ )t²]}

Interesting Features

This plot shows a double helix. The plot contains the standard helix and a second helix rotated Pi radians around. This is very similar to the double helix structure found in human DNA.