Function

[ x(t) = p cos(t), y(t) = q sin(t), z(t) = rt ]

Domain

t is an element of the set of all Real numbers

Graphs

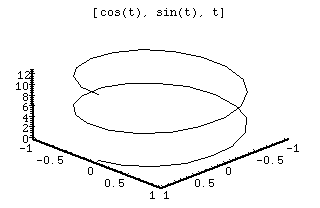
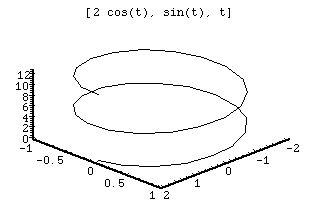
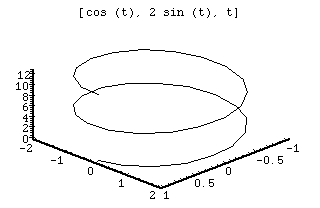
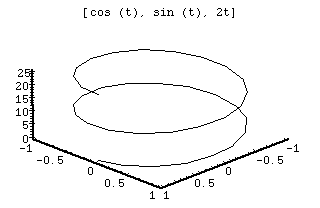
Derivative

With respect to t: [-p sin(t), q cos(t), r]

With this derivative, the only place that can have a minimum or maximum is where all the parts of the derivative are 0. Since r is some non-zero constant, there are no critical points.

Integral

With respect to t: [p sin(t), -q cos(t), ( ¹/₂ )rt²]

Interesting Features

This plot is of a curve. This curve is known as a helix. The helix forms a spring like shape. The function is in parametric form. The x and y values simply form a circle while the last value causes the circles to "rise" as they are formed creating this helix. The values for p and q stretch the circles to ellipses while the r value stretches the helix up and down.