Function

f(x,y) = sin(sqrt(x² + y²))

Domain

x and y are elements of the set of all Real numbers

Graphs

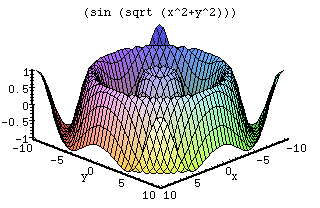
Derivative

With respect to x: (cos(sqrt(x² + y²))x)/(sqrt(x² + y²))
With respect to y: (cos(sqrt(x² + y²))y)/(sqrt(x² + y²))

Critical points are formed where the two derivatives equal 0. These critical points may be minimums, maximums, or saddle points. When looking at the first derivative, the value can be 0 when x is 0 and y is not 0, since (0,0) would make the function undefined. The other case is when the square root of the squared sum is 0. This happens at the top and bottom of all the circles. This is the same for the second partial derivative. Thus, the minimums and maximums occur at the places where the cosine of the square root of the squared sum is 0.

Integral

This integral is beyond my comprehension and computational skills. Thus I turned to the power of the Maple software program. When I asked the program to evaluate the integral, it simply returned the notation, not the answer.

Interesting Features

When working with this function, there are many different items to look at. This curve shows a sine function that radiates out from the center. The values go from -1 to 1 since it is the sine function and simply takes the positive average by taking the square root of the squared sum. The first large ring that reaches a value of 1 occurs when 1 = sin(Pi/2) = sqrt(x² + x²), with x = ^Pi/_{(2 sqrt(2))}.